上兩篇「新手專題」文章,已經分別概述了區塊鏈和加密貨幣兩者。今次講解的內容也許比較簡單,但是鑽研起來也可以相當艱深:他們就是公鑰(Public Key)和私鑰(Private Key)了。
在這篇新手專題當中,你將能夠掌握:
- 公鑰與私鑰
- 從公鑰變成錢包地址的過程
- 公鑰加密(public-key cryptography)技術
- 公鑰加密在加密貨幣領域的應用範例
(本篇文章牽涉私鑰範例。閣下請勿取用私鑰範例作儲存資產用途,如招致損失,《幣訊》概不負責。)
公鑰與私鑰
如果要使用和交易加密貨幣,應用公鑰與私鑰可以說是必須的,而公鑰和私鑰都是隸屬於「密鑰」(又稱金鑰,英文 “Key”)的種類。
在密碼學當中,金鑰的作用是用作加密(encryption)或者解密(decryption)。如果是在加密過程的話,金鑰就是將明文(Plaintext)轉化成密文(Ciphertext);相反如果是在解密過程的話,金鑰就是將密文轉化成明文。除了加密和解密之外,金鑰亦可以用於數碼簽章(Digital Signature)當中,而數碼簽章跟加密貨幣應用的關係就更加密切了 - 數碼簽章的部分,將會留在後面再講述。
來到這裡,我們應該如何理解公鑰和私鑰呢?如果以比較顯淺和籠統的例子說明,就是電子郵件:你擁有一個電子郵件郵箱,只要掌握到電郵地址,那就任何人都可以寄電郵給你,我們可以理解電郵地址就是公鑰。但是,電郵郵箱是被鎖上的,只有擁有登入密碼的人才能夠打開電郵郵箱,閱覽當中的內容,我們可以理解登入密碼就是郵箱鑰匙,也就是私鑰。
如以更簡單的講法概述,加密貨幣領域的公鑰,是為了負責對外溝通,讓外界能夠與你接觸,包括收取加密貨幣。私鑰就是為了行使權力,包括動用資產的關卡。所以如果讓人掌握你的私鑰,就等於你「容許」別人用你的錢了。
來到這裡,大家也許會問,自己的比特幣(Bitcoin, BTC)錢包地址,是不是就直接等於是公鑰呢?
- 其實也不完全是。為甚麼?
從公鑰變成錢包地址的過程
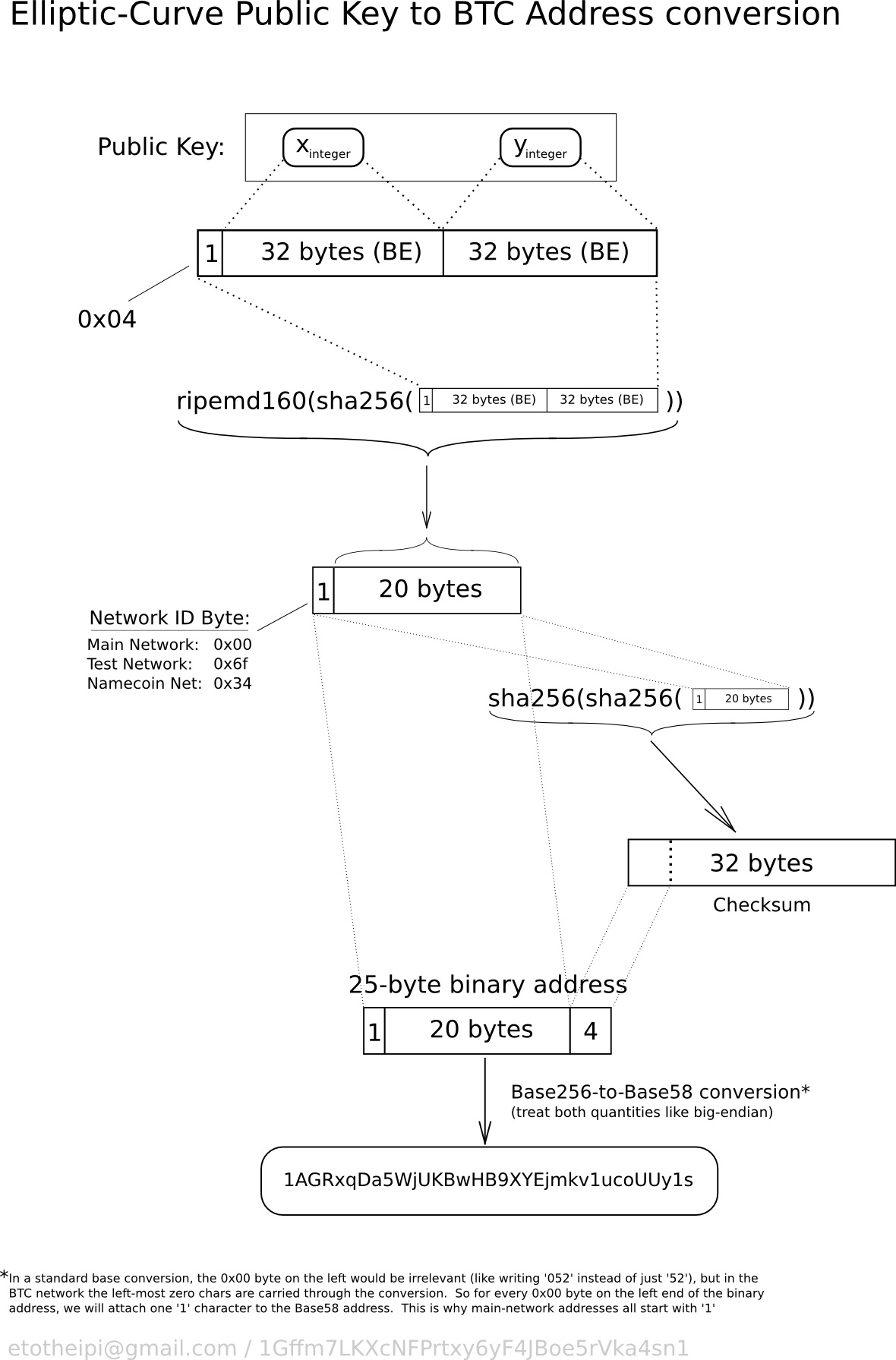
大家可以記著一點:比特幣的錢包地址,其實是雜湊函式化 / 散列化版本(hashed version)的公鑰。那麼公鑰是如何以雜湊函式,轉化成為錢包地址呢?以比特幣的平台環境為例,步驟如下:
- 首先,擁有一個 ECDSA(Elliptic Curve Digital Signature Algorithm, 橢圓曲線數字簽名算法)私鑰,例如是“7BFB502B836AADCF597BD0853A9A4E0F204CFA38AE0785FAEAE73E2F0FA7C80B”。
- 之後,將這個 ECDSA 私鑰變成 ECDSA 公鑰,即“049147785C2C22C76239ED2E5EF608E973163C3C3628FD9354BEBAD8C592E
0252859E8F210E1D90CA024D76288BF81F30A0739CEFC72BA648183F66A39064E699C”。 - 將以上的 ECDSA 公鑰,以 256 位元的 SHA-256(Secured Hash Algorithm 256, 安全雜湊演算法 256)演算法處理,變成了“6ECB94AB545E92D8A6398423EB8785055C00D8949F99ABF0B3605ABE2214B3EC”。
- 將(3)的結果,以 160 位元的 RIPEMD-160(RACE Integrity Primitives Evaluation Message Digest 160, RACE 原始完整性校驗訊息摘要 160)演算法處理,變成“227D664438579A216E329751D6507D1C3EF9B5F2”。
- 將(4)的結果,前置一個網絡位元(Network Byte)。如果是用於比特幣主網,就前置 “00”,使其變成“00227D664438579A216E329751D6507D1C3EF9B5F2”。
- 將(5)的結果,以 SHA-256 演算法處理,變成了“83428FEC0372AD1A3D578215708235A44F7A23D0E3EBA77839DD516C1D7EF575”。
- 將(6)的結果,再以 SHA-256 演算法處理,變成了“3BCCC78D8C67A0504B0AA54C6D0CB8A258D83307A2B8D12F9DD24FFBB8111E9E”。
- 從(7)的結果取出頭四位元的字碼,即 “3BCCC78D”。這四位元字碼其實是「地址校驗碼」(address checksum code)。
- 重覆填上(5)的結果,並且後置(8),即變成“00227D664438579A216E329751D6507D1C3EF9B5F23BCCC78D”。來到這裡,其實已經產生出一條 25 位元,50 字節的二進制比特幣錢包地址。
- 最後將(9)的結果,以 “Base58” 編碼方式生成正式的比特幣錢包地址,即“149NCRz2WHvLTSvTm3iXP1Vg6nu7CgpHmn”。
網上已經有一些把以上過程一鍵轉化的網站,大家不妨試試。另外如果想理解轉化過程應用過的各種算法,也可以繼續在網上搜尋,這裡則暫不討論了。
在比特幣領域當中,不論公鑰和私鑰,其實都是屬於 256 位元的數字。如果以十六進制(hexadecimal)計,公鑰和私鑰都會是 32 位元組(32 bytes),64 字節,例如上面提到,經過 SHA-256 處理的公鑰
“6ECB94AB545E92D8A6398423EB8785055C00D8949F99ABF0B3605ABE2214B3EC”。
公鑰加密技術
加密貨幣,是使用公鑰加密(public key cryptography)運作。公鑰加密又稱為非對稱加密(asymmetric cryptography)。非對稱加密的關鍵在於,加密過程是透過公鑰進行,但是解密過程是透過私鑰進行。如果加密和解密都是透過私鑰的話,那就是對稱加密(symmetric cryptography)了。
以下可以提供一個典型的公鑰加密範例:
- Alice 與 Bob 事先互不認識,也沒有可靠安全的溝通管道,但 Bob 現在卻要透過不安全的網際網路向 Alice 傳送資訊。
- Bob 撰寫好原文,內容是 “Hello Alice!”。原文在未加密的狀態下稱之為「明文」。
- Alice 使用「密碼學安全偽亂數生成器」,產生一對金鑰,其中一個作為公鑰 c,另一個作為私鑰 d。
- Alice 可以用任何方法傳送公鑰 c 給 Bob,即使 Eve 在中間竊聽到公鑰 c 都沒問題。
- Bob 用公鑰 c 把明文 “Hello Alice!” 進行加密,得到密文 “6EB6957008E03CE4”。
- Bob 可以用任何方法傳輸密文 “6EB6957008E03CE4” 給 Alice,即使 Eve 在中間竊聽到密文都沒有問題。
- Alice 收到密文,用私鑰 d 將 Bob 的密文 “6EB6957008E03CE4” 解碼,最終獲得 Bob 的明文 “Hello Alice!”。
- 由於 Eve 沒有 Alice 的私鑰 d,所以 Eve 不知道 Bob 送出的明文內容。
如果 Bob 日後想翻查曾經寫過的原文,但又遺失了自己的拷貝,除非她獲得 Alice 的私鑰 d,否則他的處境就會如 Eve 一樣,將以後無法掌握原文。
以上是典型的公鑰加密範例。但如果套用在加密貨幣,例如比特幣的交易,情況就會有些不同。

公鑰加密在加密貨幣領域的應用範例
如果大家還記得第一篇「新手專題」文章的內容,我們都曾經提及過如何產生一宗比特幣交易。在此想再一次舉例,讓大家更加明白概念。
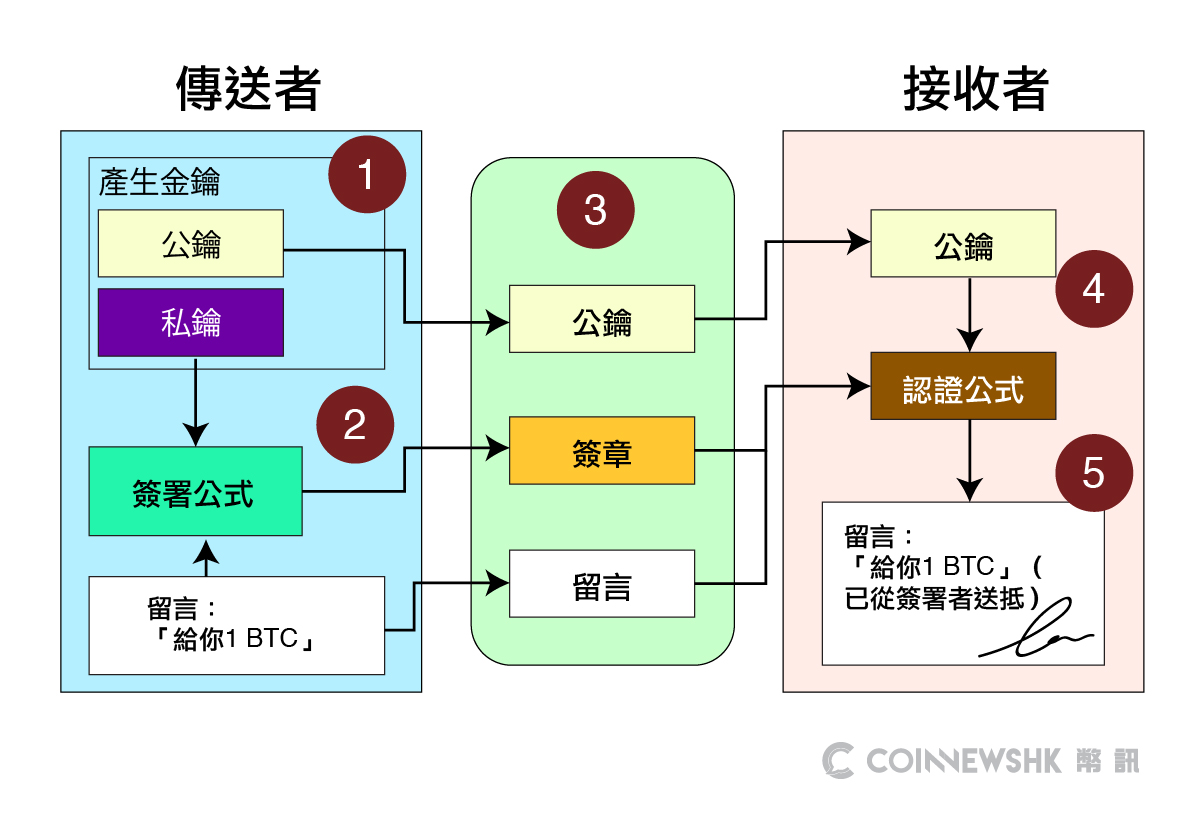
處境:大雄收到叮噹的 1.2 BTC。現時大雄想將當中的 1 BTC 傳給靜宜。以下是大雄傳送 BTC 給靜宜的過程:
- 大雄擁有上一次跟叮噹交易的內容,以及靜宜的公鑰,並變成了一節雜湊函數(Hash)。
- 大雄以自己的私鑰簽署交易。透過簽署造成的數碼簽章,其實是(1)的所有內容,並跟隨在 1 BTC 的末尾。
- 大雄的公鑰、1 BTC,以及數碼簽章,一併進入傳輸過程。
- (3)的內容已經傳輸至靜宜的錢包。靜宜取得了大雄的公鑰,並利用它來驗證簽章的內容,確認大雄是傳輸 1 BTC 給自己,過程中沒有任何篡改。
- 驗證完畢,靜宜正式獲得 1 BTC。
大家看到這裡,或者都會留意到靜宜其實不需要用上自己的私鑰都可以獲得大雄給她的 1 BTC。不過,我們仍然會說到 BTC 是使用「公鑰加密」方式運作的 - BTC 用到的 ECDSA 算法,其實是公鑰加密算法之一。
總結
有一條問題也許不少人都曾經問過:如果不見了錢包的私鑰,到底能否透過暴力破解,即利用電腦算力不停運算找出正確答案呢?我們的答案是,幾乎不可能。為何是「幾乎不可能」呢?因為能夠成功破解的機會確實低得驚人,其實是 1 / 2256,也即是 1 / 1.16 x 1077。可以說,能夠中六合彩頭獎的機會(1 / 1.398 x 107),仍然比找到私鑰的機會還要高太多太多。如果還能夠找出私鑰,也許你已經用上很多輩子的運氣……
所以,大家請務必好好保管自己的錢包私鑰呢。
以上內容由《幣訊》與 9up.io 共同協作撰寫。
【若你喜歡幣訊的內容,請輕按以下拍手鍵(可以按幾次)支持我們。】


